Matriste Toplama-Çıkarma-Çarpma (Ders 2)
Verilen Denklemleri Matrise Çevirme

Yukarıdaki denklemleri matrise çevirdiğimizde aşağıdaki sonuç ortaya çıkar

Denklemleri matrise çevirmek için bilinmeyen denklerim önündeki kat sayıları matriste uygun bir şekilde yerleştiririz. Eğer eşitlikleri de matrise dahil etmek istiyorsak : koyup yanına yazarız. Böyle yazdığımızda matrisin adı genişletilmiş matris sistemi olarak adlandırılır. C deki denklemde görüldüğü gibi denklemde bilinmeyen gözükmez ise matrise onun yerine sıfır yazarak. Çünkü onun kat sayısı sıfır olduğu için yazılmamıştır denklemde.
Matriste Toplama-Çıkarma İşlemleri nasıl yapılır?
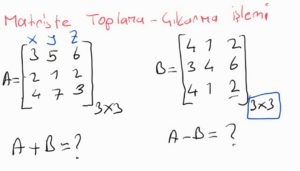
Yukarıdaki A matrisi ile B matrisini topladığımızda aşağıdaki sonuç ortaya çıkar.
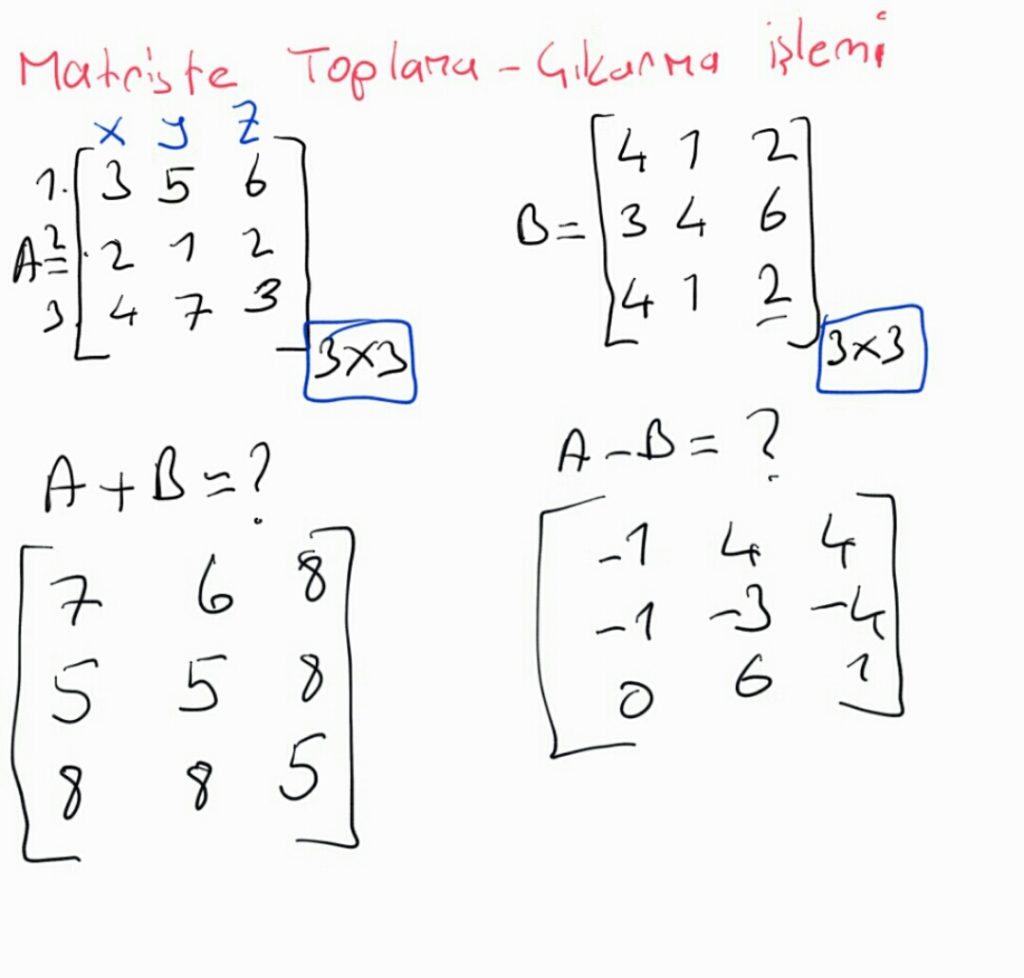
Burada dikkat etmemiz gerekenler iki matrisinde satır ve sütunları eşit olmalı. Anca eşit olursa satır ve sütunları kendi aralarında toplayıp veya çıkarabiliriz. Burada da görüldüğü gibi A matrisin 1. satır 1. sütun ile B matrisin 1. satır ile 1. sütunu topladığımızda 7 çıkardığımızda ise -1 çıkar ve diğerleri de aynı şekilde işleme sokulur.
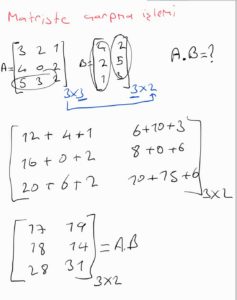
Matriste Çarpma İşlemleri nasıl yapılır?
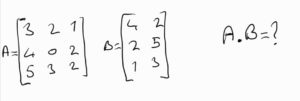
Yukarıdaki işlemi adım adım yapacak olursak aşağıdaki gibi ilk matrislerin satır ve sütunlarını belirlemeliyiz. 1. matrisin sütun sayısı ile 2. matrisin satır sayısı birbirine eşit olmalı. Eşit ise ortaya çıkacak yeni matrisin boyutu ise yanlarındaki 1. matrisin satır sayısı 2. matrisin sütun sayısına eşittir.
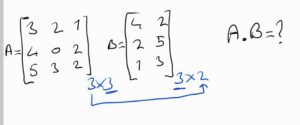
Görüldüğü gibi yukarıdaki matrislerin satır ve sütunu eşit. Buradaki işleme göre ortaya çıkacak matrisin boyutu 3×2 lik matris. Çarpmaya devam ettiğimizde ise
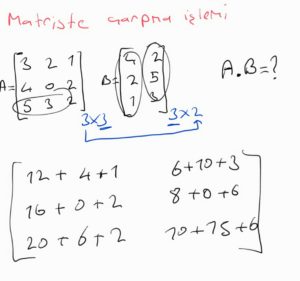
Burada 1. matrisin satırı ile 2. matrisin sütunu kendi aralarında çarpılır ve sonuçlar toplanır. Çıkan sonuç ise yeni matriste yerine yazılır. Buradaki işleme göre en sonda yeni matrisimiz aşağıdaki gibi olur.
Lineer Cebirde hangi konular var öğrenmek için lineer denklem sistemleri giriş dersine göz atabilirsiniz..
Daha detaylı öğrenmek istiyorsanız eğitim videosuna göz atabilirsiniz.