Gauss Jordan Metodu ile Denklem Çözme (Ders 6)

Gauss Jordan metodunda bilinmesi gerekilen matrisimiz indirgenmiş eşelon formda olması gerekmektedir. İndirgenmiş eşelon formda sıkıntı yaşıyorsanız İndirgenmiş eşelon form konusuna bakabilirsiniz. Bunu örnek soru ile anlamaya çalışalım.
Gauss Jordan Metodu Örnek Soru

Yukarıdaki örneği adım adım çözelim.
1) Denklemler ilk matris haline getirilir.

2) ilk satırdaki 1. eleman pivot eleman 1 olmalı ve onla kendi sütundaki altta kalanları 0 yapalım. Satır1’deki 1. elemanın altında 2 ve 1 var bunları 0 yapmak için Satır1 deki elemanları ilk -2 ile çarp ve Satır2 ile topla ve sonra Satır1 i -1 ile çarp Satır3 ile topla

3) ilk sütunumuzu indirgeme formuna soktuk şimdi 2. sütundaki pivot eleman olan Satır2 2. eleman 1 olmasaydı ilk 1 yapacaktık sonra kendi sütundaki diğer elemanları 0 yapmak için gerekli işlemleri yapacağız. Burada kendi sütunda sadece Satır3 deki 2. elemanda 1 var onu sıfır yapmak için Satır2 yi -1 ile çarp ve Satır3 ile topla.

4) Satır3 deki pivot elemanı elde etmek için Satır3 ü 3 ile bölersek pivot eleman çıkar.
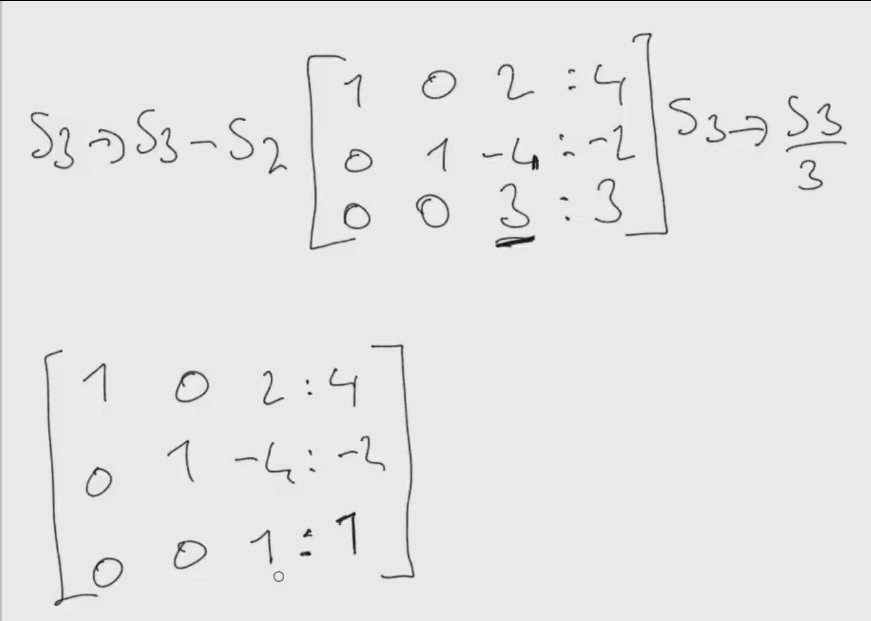
5) Satır3 deki pivot eleman ile kendi sütundaki diğer elemanları 0 yapmak için Satır2 3. eleman 0 olması için Satı3 ü 4 ile çarp Satı2 ile topla, Satır1 deki 3. elemanın 1 olması için Satır3 ü -2 ile çarp Satır1 ile topla
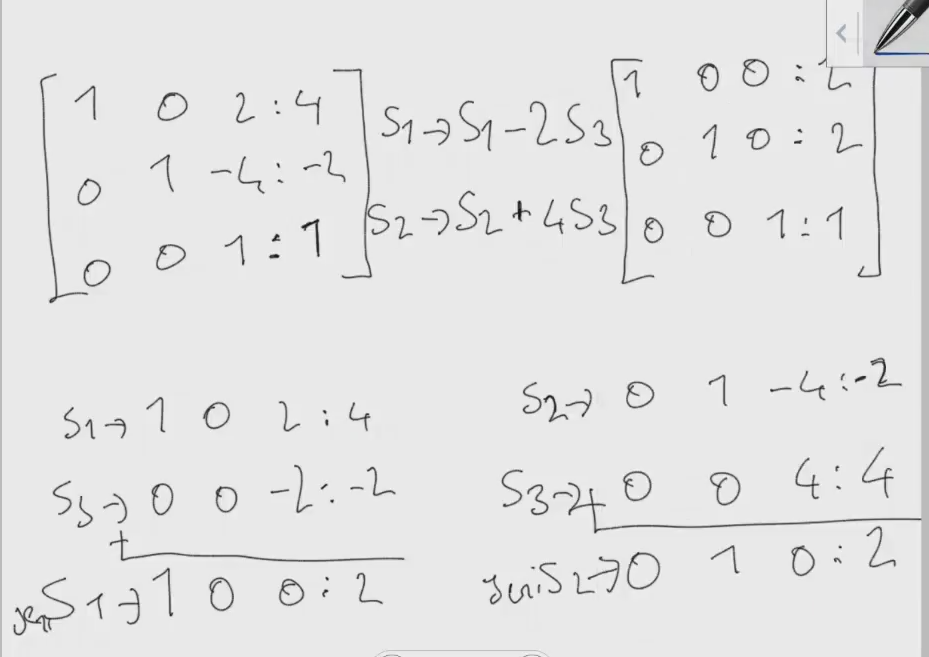
6) Son olarak matris indirgenmiş forma kavuştuğu için artık denklemin eşitlikleri çıktı.